0-1背包问题

0-1背包问题基本思想：

p[i,j]表示在前面i个物品总价值为j时的价值最大值。str[i, j]表示在前面i个物品总价值为j时的价值最大值时的物品重量串。

i=0 或者j=0时:

p[i, j] = 0;

str[i, j] = "";

第i件物品的在重量小于j时能够放入背包

p[i, j] = p[i - 1, j - w[i - 1]] + v[i - 1] > p[i - 1, j] ? p[i - 1, j - w[i - 1]] + v[i - 1] : p[i - 1, j];

 str[i, j] = p[i - 1, j - w[i - 1]] + v[i - 1] > p[i - 1, j] ? str[i - 1, j - w[i - 1]] + w[i - 1].ToString() : str[i-1,j];

第i件物品的在重量大于j时不能够放入背包：

 p[i, j] = p[i, j - 1];

str[i, j] =str[i-1,j];

代码例如以下：

class Program

    {

        //0-1背包问题

        static void Main(string[] args)

        {

            int[] w = { 2,2,6,5,4};

            int[] v = { 6, 3, 5, 4, 6 };

            String[,] str = getPackage(w,v,10);

            for (int i = 0; i < str.GetLength(0); i++)

            {

                for (int j = 0; j < str.GetLength(1); j++)

                    Console.WriteLine(i+" "+j+" 放入货物重量："+str[i,j]);

            }

            Console.Read();

        }

        static String[,] getPackage(int[] w, int[] v, int maxWeight)

        {

            int[,] p = new int[w.Length + 1, maxWeight + 1];

            String[,] str = new String[w.Length + 1, maxWeight + 1];

            for (int i = 0; i < p.GetLength(0); i++)

            {

                for (int j = 0; j < p.GetLength(1); j++)

                {

                    if (i == 0 || j == 0)

                    {

                        p[i, j] = 0;

                        str[i, j] = "";

                    }

                    else

                    {

                        if ((j - w[i - 1]) >= 0)//第i件物品的在重量小于等于j时能够放入背包

                        {

                            p[i, j] = p[i - 1, j - w[i - 1]] + v[i - 1] > p[i - 1, j] ? p[i - 1, j - w[i - 1]] + v[i - 1] : p[i - 1, j];

                            str[i, j] = p[i - 1, j - w[i - 1]] + v[i - 1] > p[i - 1, j] ? str[i - 1, j - w[i - 1]] + w[i - 1].ToString() : str[i-1,j];

                        }

                        else//第i件物品在重量大于j时不能放入背包。此时的总价值为重量为j-1时的总价值，总货物为不放入第i件物品时的总货物

                        {

                            p[i, j] = p[i, j - 1];

                            str[i, j] =str[i-1,j];

                        }

                    }

                }

            }

            return str;

        }

    }

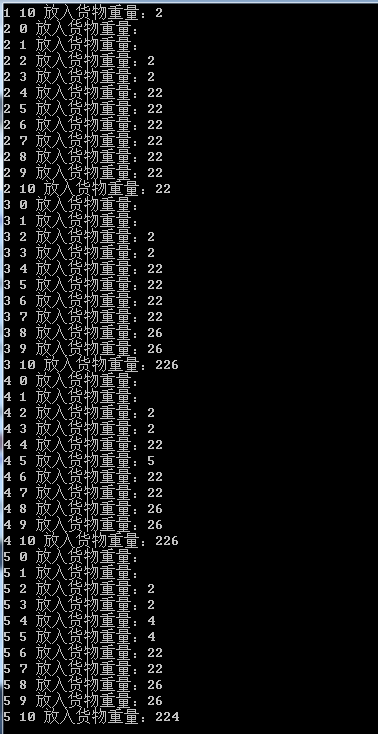
測试结果例如以下图：